|
(32.31) |
Определение 3. Пусть действительная функция f определена в некоторой окрестности точки x0 и имеет в этой точке производные всех порядков. Тогда ряд
|
(32.31) |
называется ее рядом Тейлора в точке x0.
Согласно теоремам 4 и 5 всякая
действительная аналитическая в некоторой точке
действительной оси функция (32.25) бесконечно
дифференцируема в этой точке и раскладывается в
ее окрестности в свой ряд Тейлора. Если же
функция бесконечно дифференцируема в какой-то
точке, то может случиться, что она не равна сумме
своего ряда Тейлора ни в какой окрестности этой
точки (в этом случае функция в силу сказанного
выше заведомо не аналитическая в
рассматриваемой точке).
Приведем пример такой функции.
Пример. Пусть
|
(32.32) |
Если x![]() 0, то
0, то
f'(x) = ![]()
![]() , f''(x)=
-
, f''(x)=
-![]()
![]() +
+ ![]()
![]() ,
,
вообще,
f (n)(x) = Pn(1/x) |
(32.33) |
где Pn(t) - некоторый многочлен от переменной t (n - его порядковый номер, а не степень), т. е. f (n)(x) имеет вид
f(n)(x) = ![]()
![]()
![]() kxk,
kxk, ![]() k
k ![]() R,
mn
R,
mn ![]() N.
N.
Найдем предел
![]() f (n)(x).
f (n)(x).
(Заметим, что поскольку здесь производные f (n)(x),
n = 1, 2, ..., определены пока только при x![]() 0, то здесь и ниже предел
берется по x
0, то здесь и ниже предел
берется по x![]() 0.)
Сделав замену переменной t =1/x2,
получим
0.)
Сделав замену переменной t =1/x2,
получим
![]() , m
, m
![]() N.
N.
Отсюда в силу (32.33) имеем
|
(32.34) |
Теперь, заметив, что ![]()
![]() = 0 = f(0),
т. е. что функция f непрерывна в точке x = 0,
получим отсюда (см. следствие 2
теоремы 3 из п. 12.2), что она и
дифференцируема в этой точке и что (в силу (32.34)
при n = 1) f'(0) = 0. Следовательно,
согласно (32.34) производная f' также
непрерывна при x = 0. Повторив аналогичное
рассуждение для производной f' вместо
функции f, получим, что в точке x = 0
существует вторая производная f'', что f''(0)
= 0 и что f'' непрерывна при x = 0.
Продолжая это процесс, докажем, что при любом n = 1,
2, ... имеет место равенство
= 0 = f(0),
т. е. что функция f непрерывна в точке x = 0,
получим отсюда (см. следствие 2
теоремы 3 из п. 12.2), что она и
дифференцируема в этой точке и что (в силу (32.34)
при n = 1) f'(0) = 0. Следовательно,
согласно (32.34) производная f' также
непрерывна при x = 0. Повторив аналогичное
рассуждение для производной f' вместо
функции f, получим, что в точке x = 0
существует вторая производная f'', что f''(0)
= 0 и что f'' непрерывна при x = 0.
Продолжая это процесс, докажем, что при любом n = 1,
2, ... имеет место равенство
f (n)(0) = 0.
Из него следует, что все члены ряда Тейлора функции (32.32) равны нулю, т. е. указанный ряд имеет вид
0 + 0+ ... + 0 +...,
а поскольку сама функция f(x)![]() 0 при x
0 при x![]() 0, то она не равна сумме своего ряда
Тейлора ни в какой окрестности точки x = 0.
Функция (32.32) является примером бесконечно
дифференцируемой функции, не являющейся
аналитической в данной точке. То, что она
бесконечно дифференцируема в точке x = 0,
только что было доказано, а то, что она
неаналитическая в данной точке (т. е. не
раскладывается в степенной ряд), следует из того,
что она ни в какой окрестности нуля не является
суммой своего ряда Тейлора в этой точке.
0, то она не равна сумме своего ряда
Тейлора ни в какой окрестности точки x = 0.
Функция (32.32) является примером бесконечно
дифференцируемой функции, не являющейся
аналитической в данной точке. То, что она
бесконечно дифференцируема в точке x = 0,
только что было доказано, а то, что она
неаналитическая в данной точке (т. е. не
раскладывается в степенной ряд), следует из того,
что она ни в какой окрестности нуля не является
суммой своего ряда Тейлора в этой точке.
Пусть f - бесконечно
дифференцируемая в точке x0 функция,
|
(32.35) |
- ее ряд Тейлора,
sn(x) = |
(32.36) |
- частичная сумма порядка n = 1, 2, … ряда (32.35) и
rn(x) = f(x) - sn(x) |
(32.37) |
- остаточный член формулы Тейлора для функции f (а не сумма остатка ряда (32.35), так как сумма остатка ряда имеет смысл только тогда, когда известно, что ряд сходится; относительно же ряда (32.35) это не предполагалось. Кроме того, если он даже и сходится, то неизвестно, равна его сумма f(x) или нет). Таким образом,
f(x) = sn(x) + rn(x) |
(32.38) |
- формула Тейлора для функции f.
Отсюда видно, что для того чтобы
функция f равнялась сумме своего ряда Тейлора
в некоторой точке x, надо, чтобы в этой точке
остаточный член формулы Тейлора (32.38)
стремился к нулю при n![]()
![]() :
:
|
(32.39) |
В самом деле, если это имеет место, то из формулы (32.38) следует, что
f(x) =![]() sn(x),
sn(x),
т. е. f(x) является суммой
ряда (32.35).
Для исследования свойства (32.39)
остаточного члена rn(x) установим
некоторые новые виды его записи. Напомним
предварительно, что если точка ![]() принадлежит интервалу с концами в
точках x0 и x, т. е. либо x <
принадлежит интервалу с концами в
точках x0 и x, т. е. либо x < ![]() < x0,
либо x0 <
< x0,
либо x0 < ![]() < x, и если
< x, и если ![]() = (
= (![]() - x0)/(x - x0),
то
- x0)/(x - x0),
то ![]() = x0+
= x0+![]() (x - x0),
0 <
(x - x0),
0 < ![]() <1.
<1.
Теорема 6. Если функция f
n + 1 раз непрерывно
дифференцируема на интервале} (x0 - h, x0 + h),
h > 0, то остаточный член rn(x)
ее формулы Тейлора (32.38) для всех x ![]() (x0 - h, x0 + h)
можно записать в каждом из следующих трех видов:
(x0 - h, x0 + h)
можно записать в каждом из следующих трех видов:
где ![]() принадлежит
интервалу с концами в точках x0 и x, т. е.
принадлежит
интервалу с концами в точках x0 и x, т. е.
![]() = x0 +
= x0 + ![]() (x - x0),
0 <
(x - x0),
0 < ![]() < 1, и
< 1, и
где 0 <![]() < 1.
< 1.
Формула (32.40) называется остаточным
членом формулы Тейлора в интегральной форме,
формула (32.41) - в форме Лагранжа, а (32.42) - в
форме Коши.
Число ![]() , 0 <
, 0 < ![]() < 1, участвующее в
записи остаточного члена rn(x),
зависит от x и от n.
< 1, участвующее в
записи остаточного члена rn(x),
зависит от x и от n.
![]() В силу формулы
Ньютона - Лейбница имеем
В силу формулы
Ньютона - Лейбница имеем
f(x) = f(x0) +![]() f'(t)dt = f(x0)
-
f'(t)dt = f(x0)
-![]() f'(t) d(x - t).
f'(t) d(x - t).
Применив интегрирование по частям к интегралу в правой части этого равенства, получим
f(x) = f(x0) + (-f'(t)(x
- t))![]() +
+ ![]() f''(t)(x - t)dt
= f(x0) + f'(x0)(x
- x0) +
f''(t)(x - t)dt
= f(x0) + f'(x0)(x
- x0) +![]() f''(t)(x
- t)dt.
f''(t)(x
- t)dt.
Пусть для некоторого m < n уже доказано, что
f(x) = |
(32.43) |
Эта формула уже доказана нами для m = 1 и m = 2. Проинтегрируем по частям последнее слагаемое в правой части равенства
![]()
![]() f(m)(t)(x
- t)m-1dt = -
f(m)(t)(x
- t)m-1dt = -![]()
![]() f(m)(t)(x
- t)mdt =
f(m)(t)(x
- t)mdt =
= -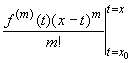 +
+ ![]()
![]() f (m+1)(t)(x
- t)mdt =
f (m+1)(t)(x
- t)mdt = ![]() (x - x0)m
+
(x - x0)m
+ ![]()
![]() f (m+1)(t)(x - t)mdt.
f (m+1)(t)(x - t)mdt.
Подставим получившееся выражение в (32.43):
f(x) = ![]()
![]() (x - x0)k
+
(x - x0)k
+ ![]()
![]() f (m+1)(t)(x - t)mdt.
f (m+1)(t)(x - t)mdt.
В результате получилась формула (32.43), в которой m
заменено на m + 1.
Таким образом, формула Тейлора (32.43)
доказана методом математической индукции для
всех m < n. При m = n
ее остаточный член имеет вид (32.40).
Применим теперь интегральную теорему
о среднем значении к интегралу (32.40).
Заметив, что функция (x - t)n
не меняет знака n, x0 и x
фиксированы, a t изменяется между x0
и x), а функция f (n+1)
непрерывна на промежутке интегрирования,
вынесем за знак интеграла "среднее
значение" производной f (n+1)
(см. следствие из
теоремы п. 24.2):
rn(x) = ![]()
![]() f (n+1)(t)(x
- t)ndt =
f (n+1)(t)(x
- t)ndt = ![]()
![]() (x - t)ndt
=
(x - t)ndt
=
= ![]()
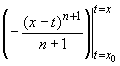 =
= ![]() (x - x0)n+1,
(x - x0)n+1,
где ![]() лежит на
интервале с концами в точках x0 и x.
Формула (32.41) доказана. Если применить
интегральную теорему о среднем к
интегралу (32.40), вынося за знак интеграла
среднее значение всей подынтегральной функции
(см. п. 24.2), то получим
лежит на
интервале с концами в точках x0 и x.
Формула (32.41) доказана. Если применить
интегральную теорему о среднем к
интегралу (32.40), вынося за знак интеграла
среднее значение всей подынтегральной функции
(см. п. 24.2), то получим
rn(x) = |
(32.44) |
где ![]() , как и выше,
лежит на интервале с концами в точках x0
и x, т. е.
, как и выше,
лежит на интервале с концами в точках x0
и x, т. е. ![]() = x0 +
= x0 + ![]() (x - x0),
0 <
(x - x0),
0 < ![]() <1. Отсюда
<1. Отсюда
x - ![]() = x - x0 -
= x - x0 - ![]() (x - x0) = (x - x0)(1
-
(x - x0) = (x - x0)(1
- ![]() ).
).
Подставив это выражение x-![]() в (32.44), получим формулу
(32.42).
в (32.44), получим формулу
(32.42). ![]()
Укажем теперь одно достаточное
условие разложимости функции в степенной ряд.
Теорема 7. Если функция в
окрестности точки x0 имеет все
производные, ограниченные в совокупности на
этой окрестности, то функция раскладывается в
степенной ряд в некоторой окрестности точки x0.
![]() Пусть функция f
имеет на интервале (x0 - h, x0 + h)
производные всех порядков и они ограничены в
совокупности на этом интервале, т. е.
существует такая постоянная c > 0, что
для всех x
Пусть функция f
имеет на интервале (x0 - h, x0 + h)
производные всех порядков и они ограничены в
совокупности на этом интервале, т. е.
существует такая постоянная c > 0, что
для всех x ![]() (x0 - h, x0 + h)
и всех n = 0, 1, 2, ... выполняется неравенство
(x0 - h, x0 + h)
и всех n = 0, 1, 2, ... выполняется неравенство
| f (n)(x)| < c. |
(32.45) |
Заметим, что
|
(32.46) |
Это следует из того, что ряд ![]() hn/n! сходится при любом z
hn/n! сходится при любом z
![]() C
C
(пример 1 из п. 31.1), в
частности, он сходится при z = h, а
равенство (32.46) выражает собой необходимое
условие сходимости этого ряда:
последовательность членов сходящегося ряда
стремится к нулю.
Для того чтобы доказать, что функция f
раскладывается в степенной ряд, т. е. в ряд
Тейлора:
|
(32.47) |
достаточно убедиться в том, что (см. (32.39))
|
(32.48) |
где rn(x) - остаточный член формулы Тейлора функции f в точке x0. Возьмем rn(x) в форме Лагранжа (см. (32.41)). Из неравенства (32.45) следует, что
|rn(x)| = |
(32.49) |
где x и ![]() таковы,
что |
таковы,
что |![]() - x0|
< |x - x0| < h. Так как
согласно (32.46) имеет место
- x0|
< |x - x0| < h. Так как
согласно (32.46) имеет место
![]()
![]() = 0,
= 0,
то в силу неравенства (32.49) при |x - x0|
< h выполняется условие (32.48). ![]()
Замечание. При доказательстве
теоремы 7 было показано, что остаток rn(x)
ряда не только стремится к нулю, но и то, что это
стремление к нулю в силу оценки (32.49)
происходит на интервале (x0 - h, x0 + h)
равномерно. Поэтому если все производные функции
f ограничены на интервале (x0 - h, x0 + h),
то ряд Тейлора в точке x0 сходится на
этом интервале к самой функции f(x)
равномерно.
Аналитические функции в действительной области Оглавление Разложение элементарных функций в ряд Тейлора