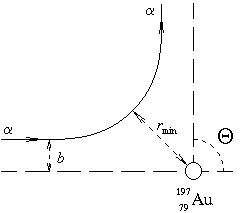
Свойства атомных ядер

1. Альфа-частицы с кинетической энергией T = 6.5 МэВ испытывают резерфордовское рассеяние на ядре золота ¹⁹⁷Au. Определить: 1) параметр столкновения b для альфа-частиц, наблюдаемых под углом  = 90⁰; 2) минимальное расстояние r_min сближения альфа-частиц с ядром; 3) кинетическую (T^') и 4) потенциальную (E^') энергии альфа-частиц в этой точке.

2. Протон с кинетической энергией T = 2 МэВ налетает на неподвижное ядро ¹⁹⁷Au. Определить дифференциальное сечение рассеяния dσ/dΩ на угол θ = 60° . Как изменится величина дифференциального сечения рассеяния, если в качестве рассеивающего ядра выбрать ²⁷Al?

3. Вычислить сечение рассеяния α-частицы с кинетической энергией T = 5 МэВ кулоновским полем ядра ²⁰⁸Pb под углами больше 90⁰.

4. Золотая пластинка толщиной l = 1 мкм облучается пучком α-частиц с плотностью потока
j = 10⁵ частиц/см²·с. Кинетическая энергия α-частиц T = 5 МэВ. Сколько α-частиц на единицу телесного угла падает в секунду на детектор, расположенный под углом θ = 170° к оси пучка? Площадь пятна пучка на мишени S = 1 см².

5. Рассчитать дифференциальное сечение dσ/dΩ упругого рассеяния протонов на ядрах золота ¹⁹⁷Au под углом 15° , если известно, что за сеанс облучения мишени толщиной d = 7 мг/см² протонами с суммарным зарядом Q = 1 нКл на детектор площадью S = 0.5 см², расположенный на расстоянии l = 30 см от мишени, попало ΔN = 1.97·10⁵ упруго рассеянных протонов. Сравнить экспериментально измеренное сечение с резерфордовским.

6. При упругом рассеянии электронов с энергией T = 750 МэВ на ядрах ⁴⁰Ca в сечении наблюдается дифракционный минимум под углом θ_min = 18° . Оценить радиус ядра ⁴⁰Ca.

7. Эмпирическая зависимость радиуса ядра R от числа нуклонов A (A > 10) R ≈ r₀A^1/3.
Параметр r₀ ≈ 1.23·10^-13 см = 1.23 Фм приблизительно одинаков для всех ядер.
Оценить радиусы атомных ядер ²⁷Al, ⁹⁰Zr, ²³⁸U.

8. Оценить плотность ядерной материи.

9. Массы нейтрона и протона в энергетических единицах равны соответственно m_n = 939.6 МэВ и m_p = 938.3 МэВ. Определить массу ядра ²H в энергетических единицах, если энергия связи дейтрона E_св(2,1) = 2.2 МэВ.

10. Масса нейтрального атома ¹⁶O m_ат(A,Z) = 15.9949 а.е.м. Определить удельную энергию связи ε ядра ¹⁶O.

11. Массы нейтральных атомов в а.е.м.: ¹⁶O - 15.9949, ¹⁵O - 15.0030, ¹⁵N - 15.0001. Чему равны энергии отделения нейтрона и протона в ядре ¹⁶O?

12. С помощью формулы Вайцзеккера рассчитать энергии отделения нейтронов в четно-четных изотопах ³⁸Ca, ⁴⁰Ca, ⁴⁸Ca.

13. Считая, что разность энергий связи зеркальных ядер определяется только различием энергий кулоновского отталкивания в этих ядрах, вычислить радиусы зеркальных ядер ²³Na, ²³Mg.
E_св(²³Na) = 186.56 МэВ, E_св(²³Mg) = 181.72 МэВ.

14. Ядро ²⁷Si в результате β⁺-распада ²⁷Si → ²⁷Al + e⁺ + ν_e переходит в "зеркальное" ядро ²⁷Al. Максимальная энергия позитронов 3.48 МэВ. Оценить радиус этих ядер.