6.9. Непрерывные функции

    Согласно определению (определение 5, п. 6.2) функция y = f(x) непрерывна в точке x₀ R, если

f(x) = f(x₀).

    Это означает (определение 1, п. 6.1), что если x_nx₀, x_n X, то f(x_n) f(x₀), n = 1, 2, ..., а также (см. определение 6 и теорему 1 в п. 6.3), что для любого > 0 существует такое , что для всех x X, удовлетворяющих условию |xx₀| < , выполняется неравенство | f(x) f(x₀)| < .
    Из (6.22) следует, что

Введем обозначения:

xx - x₀,  y f(x) - f(x₀) = f(x₀+x) - f(x₀).

Тогда равенство (6.23) можно записать в виде

    С точки зрения приближенного вычисления значений функций выполнение равенства (6.22), т. е. непрерывность функции, означает, что по достаточно точным приближенным значениям аргумента можно вычислять сколь угодно точно значения функции.
    В качестве примера использования записи условия непрерывности в виде (6.24) покажем, что функция f(x) = 1/x (рис. 63) непрерывна во всех точках
x₀0. Имеем

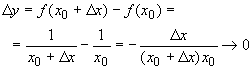
при x0.

Бывает полезным условие непрерывности функции в точке, основанное на рассмотрении предела функции по проколотой окрестности этой точки (см. определение 4 в п. 6.1).

    Лемма 5. Если функция f задана на множестве X, x₀ X и существует предел

то функция  f непрерывна в точке x₀ тогда и только тогда, когда

a = f(x₀).

    Если функция f непрерывна в точке x₀, т. е. выполняется условие (6.22), то

f(x) = f(x) =  f(x₀)

(предел по подмножеству совпадает с пределом по множеству, если последний существует). Таким образом, предел (6.25) равен  f(x₀).
    Пусть, наоборот, выполняется условие a = f(x₀), т. е.

очевидно, и

f(x) = f(x₀) =  f(x₀).

Таким образом, по двум множествам X \{x₀} и {x₀} функция  f при xx₀ имеет один и тот же предел   f(x₀). Поэтому она согласно лемме 3 из п. 6.5 имеет тот же предел и по их объединению

(X \{x₀}) {x₀} = x,

т. е.

f(x) =  f(x₀).

    Это означает, что из выполнения условия a = f(x₀) следует выполнение условия (6.22), т. е. того, что функция f непрерывна в точке x₀. 
    Условие непрерывности леммы 5 бывает полезно, в частности, в случае односторонних пределов, когда пределы слева и справа берутся по множествам, не содержащим точки x₀, т. е. когда рассматриваются пределы  f(x₀ - 0) и  f(x₀ + 0). Именно, имеет место следующее утверждение.
    Если x₀ X и

 f(x) =  f(x) =  f(x₀),

то функция  f непрерывна в точке x₀.
Действительно, из условия (6.27) следует, что =   f(x₀), а поэтому согласно лемме 5 функция  f непрерывна в точке x₀. 
    Для дальнейшего анализа свойства непрерывности функции введем понятия изолированных и предельных точек множества.

    Определение 10. Точка x₀ называется изолированной точкой множества X R, если существует окрестность U(x₀), пересечение которой с множеством X состоит только из самой точки x₀:

U(x₀) X = {x₀}.

    Определение 11. Точка x₀ называется предельной точкой множества X R, если в любой ее окрестности содержится точка множества X, отличная от самой точки x₀.
    Например, все точки множества натуральных чисел N изолированы, а множество Q всех рациональных чисел вовсе не имеет изолированных точек. Каждая точка числовой прямой R является предельной точкой для множеств Q, I и R.
    Предельная точка множества может как принадлежать самому множеству, так и не принадлежать ему. Так, например, концы a и b отрезка [a, b] и интервала (a, b) являются предельными точками и того, и другого промежутка, но в первом случае они принадлежат ему, а во втором - нет.
    Каждая точка прикосновения множества X является либо его изолированной точкой, либо его предельной точкой. В самом деле, либо у нее существует окрестность, не содержащая других точек множества, кроме нее самой, тогда она изолированная, либо в любой ее окрестности имеются точки множества X, отличные от нее, тогда она предельная.

    Лемма 6. Всякая функция непрерывна в каждой изолированной точке множества своего определения.
Пусть на множестве X задана функция f и x₀ - изолированная точка множества X. Тогда существует такая окрестность U(x₀) точки, что

U(x₀) X = {x₀}.

Какова бы ни была последовательность x_n X, n = 1, 2, ..., такая, что x_n = x₀, существует такой номер n₀, что для всех n > n₀ выполняется условие x_n U(x₀), и так как x_n X, то при n > n₀ имеет место равенство  x_n = x₀, а следовательно, и f(x_n) =  f(x₀) (т. е., начиная с номера n₀ + 1, последовательность { f(x_n)} делается стационарной), а потому f(x_n) =  f(x₀). В силу произвольного выбора последовательности x_nx₀, x_n X, n = 1, 2, ..., это означает, что

 f(x) =  f(x₀).   

    Например, функции, определенные лишь на одной точке или на двух точках, или, более общо, на любом конечном множестве точек, являются непрерывными. Непрерывной является и элементарная функция

определенная только для целочисленных значений аргумента, т. е. для x = 0, +1, +2, ..., в которых она равна 1 (в остальных точках выражение под знаком корня отрицательно, и поэтому функция не определена). График этой функции состоит из отдельных изолированных точек (0;1), (1;1), (-1;1), (2;1), (-2;1), ... (рис. 64).
    Таким образом, при изучении вопроса о непрерывности функции в некоторой точке следует рассматривать лишь предельные точки ее множества определения, так как, согласно доказанному, во всех изолированных точках этого множества она заведомо непрерывна.
    В этом смысле дискретное в математике является частным случаем непрерывного.

Бесконечно малые  Оглавление  Классификация точек разрыва