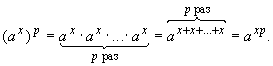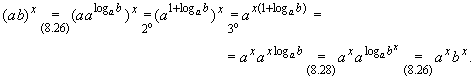8.2. Показательная и логарифмическая функции
Перечислим основные свойства
степеней ar, a > 0, с
рациональными показателями r  Q (см. п. 2.1).
Q (см. п. 2.1).
1o. Пусть r1 < r2.
Если a > 1, то 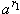 <
<
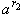 , а если a < 1, то
, а если a < 1, то
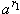 >
>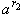 .
.
2o. 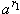
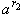 =
= 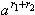 .
.
3o. 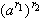 =
= 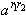 .
.
Эти свойства доказываются в курсе
элементарной математики в предположении
существования и однозначной определенности ar
для любого рационального r, a > 0, а
это было доказано в п. 7.3.
Вспомним еще, что a0 = 1 и
что a-r = 1/r.
Из свойства 1o вытекает, что для
любого r  Q выполняется неравенство ar > 0.
В самом деле, если a > 1 и r > 0,
то по свойству 1o ar > a0 = 1 > 0.
Отсюда следует, что a-r = 1/r > 0.
Аналогично рассматривается случай 0 < a < 1.
Q выполняется неравенство ar > 0.
В самом деле, если a > 1 и r > 0,
то по свойству 1o ar > a0 = 1 > 0.
Отсюда следует, что a-r = 1/r > 0.
Аналогично рассматривается случай 0 < a < 1.
Нашей ближайшей задачей является
определение значения выражения ax для
любого действительного числа x и a > 0.
Затем будут изучены свойства функции ax.
Лемма 1. Для любого a > 0
имеет место равенство
 a1/n
= a1/n
= 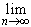 a-1/n = 1. a-1/n = 1.
|
(8.1) |
Следствие. Для любого a > 0
имеет место равенство
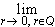 ar = 1. ar = 1.
|
(8.2) |
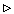 Пусть сначала a > 1.
Для любого n
Пусть сначала a > 1.
Для любого n  N положим
N положим
Поскольку 1/n > 0, то a1/n > a0
и, следовательно,
xn > 0, n = 1,
2, ... |
(8.4) |
Из (8.3) и (8.4) вытекает, что
a = (1 + xn)n = 1
+ nxn + ... > nxn.
Отсюда и из неравенства (8.4) получаем 0 < xn < a/n,
а так как 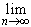 (a/n) = 0,
то
(a/n) = 0,
то 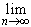 xn = 0, что в
силу (8.3) и означает, что
xn = 0, что в
силу (8.3) и означает, что
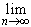 a1/n
= 1. a1/n
= 1.
|
(8.5) |
Если a < 1, то b = 1/a > 1, и потому
Наконец, если a = 1, то утверждение (8.1)
очевидно, так как
11/n = 1, n = 1, 2,
...
Из доказанного следует, что при любом a > 0
имеет место и равенство
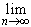 a-1/n
= 1/
a-1/n
= 1/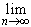 a1/n = 1.
a1/n = 1.
Докажем следствие.
 Для всех a > 0
функция ar монотонна на множестве
рациональных чисел Q.
Для каждого действительного числа x
множества рациональных чисел r < x
и r > x не пусты и точка x
является их точкой прикосновения. Поэтому,
согласно следствию из теоремы 4
п. 6.11, существуют односторонние пределы
Для всех a > 0
функция ar монотонна на множестве
рациональных чисел Q.
Для каждого действительного числа x
множества рациональных чисел r < x
и r > x не пусты и точка x
является их точкой прикосновения. Поэтому,
согласно следствию из теоремы 4
п. 6.11, существуют односторонние пределы 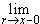 ar
ar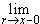 ar и
ar и 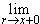 ar,
r
ar,
r  Q. В частности, указанные
пределы существуют для x = 0. Согласно
определению предела функции в терминах
последовательностей их значения равны
соответственно значению последовательностей
Q. В частности, указанные
пределы существуют для x = 0. Согласно
определению предела функции в терминах
последовательностей их значения равны
соответственно значению последовательностей 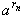 при любых последовательностях rn < 0
и rn > 0, стремящихся к нулю, rn
при любых последовательностях rn < 0
и rn > 0, стремящихся к нулю, rn  Q,
n = 1, 2, ... Выбрав rn = -1/n
и rn = 1/n, для которых
пределы уже вычислены (см. (8.1)), в силу сказанного
получим
Q,
n = 1, 2, ... Выбрав rn = -1/n
и rn = 1/n, для которых
пределы уже вычислены (см. (8.1)), в силу сказанного
получим
т. е. односторонние пределы в точке x = 0
функции ar, r  Q, r
Q, r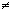 0, равны и, следовательно,
согласно теореме 2 п. 6.6,
существует двусторонний предел
0, равны и, следовательно,
согласно теореме 2 п. 6.6,
существует двусторонний предел 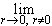 ar = 1 . Он
совпадает со значением a0 = 1
функции ar при r = 0, а поэтому (см. лемму 5 в п. 6.9) она
непрерывна в нуле:
ar = 1 . Он
совпадает со значением a0 = 1
функции ar при r = 0, а поэтому (см. лемму 5 в п. 6.9) она
непрерывна в нуле:
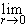 ar = a0 = 1,
r
ar = a0 = 1,
r  Q, a > 0.
Q, a > 0.
Равенство (8.2) доказано. 
Определение. Пусть a > 0 и x  R.
Определим ax как предел ar по
множеству рациональных чисел Q,
когда r
R.
Определим ax как предел ar по
множеству рациональных чисел Q,
когда r x, т. е.
x, т. е.
ax  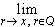 ar. ar. |
(8.7) |
Докажем, что это определение
корректно, т. е. покажем, используя критерий
Коши для предела функции (см. теорему 5 в п. 6.12), что предел (8.7)
существует.
 Пусть a > 1 и x
Пусть a > 1 и x  R.
В силу принципа Архимеда существует натуральное n
такое, что
R.
В силу принципа Архимеда существует натуральное n
такое, что
Зададим произвольно  > 0. Согласно следствию леммы 1
существует такое
> 0. Согласно следствию леммы 1
существует такое  > 0,
что для всех рациональных r, удовлетворяющих
неравенству
> 0,
что для всех рациональных r, удовлетворяющих
неравенству
|r| <  , , |
(8.9) |
выполняется неравенство
|ar - 1| <  /an. /an. |
(8.10) |
Если это условие выполняется для некоторого  > 0, то оно заведомо
выполняется и для всякого меньшего
положительного
> 0, то оно заведомо
выполняется и для всякого меньшего
положительного  .
Поэтому указанное
.
Поэтому указанное  > 0
можно всегда выбрать так, чтобы выполнялось
неравенство (см. (8.8))
> 0
можно всегда выбрать так, чтобы выполнялось
неравенство (см. (8.8))
x +  /2 < n. /2 < n. |
(8.11) |
Если рациональные числа r' и r"
принадлежат  /2-окрестности
точки x:
/2-окрестности
точки x:
|r' - x| <  /2, |r" - x| <
/2, |r" - x| <  /2,
/2,
и, следовательно,
|r" - r'| < |r"
- x| + |x - r'| <  /2 + /2 +  /2 = /2 =  , , |
(8.12) |
то, заметив, что
r' < x +  /2 /2 |
< n , |
|
(8.22) |
будем иметь
|ar" - ar'|
= ar'|ar"-r' - 1| |
< |
an|ar"-r' - 1| |
< |
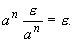
|
|
(8.8)
(8.11) |
|
(8.9), (8.10)
(8.12) |
|
Таким образом, для произвольно заданного  > 0 существует такое
> 0 существует такое  > 0, что из выполнения
условий
> 0, что из выполнения
условий
|r' - x| <  /2, |r"
- x| <
/2, |r"
- x| <  /2 вытекает
неравенство
/2 вытекает
неравенство
|ar" - ar'| <  .
.
Согласно критерию Коши это означает
существование конечного предела 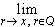 ar для всех x
ar для всех x
 R,
a > 1. Этот предел обозначается ax.
R,
a > 1. Этот предел обозначается ax.
Если 0 < a < 1, то b = 1/a > 1,
для любого x  R предел
R предел
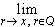 ar
= 1/
ar
= 1/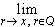 ar
ar
также существует. 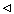
Отметим, что если x  Q, то
определение (8.7) совпадает с уже известным
определением рациональной степени ar
числа a, r
Q, то
определение (8.7) совпадает с уже известным
определением рациональной степени ar
числа a, r  Q. Действительно, в
силу доказанного предел
Q. Действительно, в
силу доказанного предел 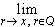 ar = ax
существует и для любой последовательности rn
ar = ax
существует и для любой последовательности rn x, rn
x, rn  Q, n = 1,
2, ..., равен пределу
Q, n = 1,
2, ..., равен пределу 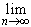
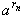 . В случае x = r
. В случае x = r
 Q
за указанную последовательность можно взять
стационарную последовательность rn = r,
n = 1, 2, ... Тогда будем иметь
Q
за указанную последовательность можно взять
стационарную последовательность rn = r,
n = 1, 2, ... Тогда будем иметь
ax = 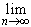
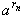 =
= 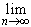 ar = ar.
ar = ar.
Из определения функции ax
следует, что для любого действительного числа x
выполняется равенство
Действительно, это равенство имеет место для
рациональных значений x = r  Q,
поэтому для любого действительного x
получаем
Q,
поэтому для любого действительного x
получаем
a-x |
= |
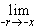 a-r = a-r =  (1/ar) (1/ar) |
= |
1/ax. |
|
(8.7) |
|
(8.7) |
|
Функция f(x) = ax,
a > 0, x  R,
называется показательной функцией.
R,
называется показательной функцией.
В случае a = e функция ex
обозначается также exp x и называется экспонентой.
Теорема 3. Показательная функция ax,
a > 0, обладает следующими свойствами.
1o. При a > 1 она
строго возрастает, а при a < 0
строго убывает на всей числовой оси.
2o. Для любых x  R
и y
R
и y  R имеет место равенство axay = ax+y.
R имеет место равенство axay = ax+y.
3o. Для любых x  R
и y
R
и y  R имеет место равенство (ax)y = axy.
R имеет место равенство (ax)y = axy.
4o. Функция ax
непрерывна на всей числовой оси.
5o. Областью значений функции ax
является множество всех положительных чисел, т. е.
бесконечный интервал (0,+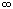 ).
).
 Доказательство.1o.
Пусть для определенности a > 1 и x < y.
Существуют такие рациональные числа r' и r",
что
Доказательство.1o.
Пусть для определенности a > 1 и x < y.
Существуют такие рациональные числа r' и r",
что
x < r' < r" < y.
Возьмем последовательности рациональных чисел
r'n x и r"n
x и r"n y такие, что r'n < r' < r" < r"n,
n = 1, 2, ... Тогда в силу свойства 1o
степеней с рациональными показателями будем
иметь
y такие, что r'n < r' < r" < r"n,
n = 1, 2, ... Тогда в силу свойства 1o
степеней с рациональными показателями будем
иметь
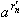 < ar'< ar" <
< ar'< ar" < 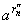 , n = 1, 2, ...
, n = 1, 2, ...
Переходя в этом неравенстве к пределу при n
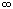 , получим
, получим
ax = 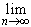
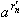 < ar'< ar" <
< ar'< ar" < 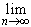
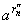 = a y,
= a y,
т. е. при x < y имеет место
неравенство ax < a y.
Отметим, что из 1o и того, что для
любого рационального r имеет место
неравенство a r > 0, следует,
что для любого действительного числа x
выполняется неравенство
В самом деле, если, например, a > 1
и x  R, то, выбрав рациональное
число r так, чтобы выполнялось неравенство r < x,
получим ax > ar > 0.
Аналогично рассматривается случай 0 < a < 1.
R, то, выбрав рациональное
число r так, чтобы выполнялось неравенство r < x,
получим ax > ar > 0.
Аналогично рассматривается случай 0 < a < 1.
Доказательство 2o. Пусть x  R,
y
R,
y  R, r'n
R, r'n  Q, r"n
Q, r"n
 Q,
r'n
Q,
r'n x и r"n
x и r"n y, и, следовательно, r'n + r"n
y, и, следовательно, r'n + r"n x + y, n = 1, 2, ...
Тогда
x + y, n = 1, 2, ...
Тогда
Доказательство 4o. (свойство 3o
будет доказано позже). Покажем, что функция ax
непрерывна на всей числовой оси. Пусть x0.
В силу монотонности функции ax (см.
свойство 1o) существуют конечные
односторонние пределы 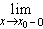 ax
и
ax
и 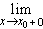 ax.
Ясно, что они совпадают соответственно с
односторонними пределами
ax.
Ясно, что они совпадают соответственно с
односторонними пределами 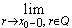 ar и
ar и 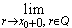 ar
сужения функции ax на множество
рациональных чисел Q,
из которого удалена точка x0, если она
рациональная. Эти пределы в свою очередь
совпадают с двусторонним пределом
ar
сужения функции ax на множество
рациональных чисел Q,
из которого удалена точка x0, если она
рациональная. Эти пределы в свою очередь
совпадают с двусторонним пределом 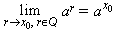 (см. формулу (8.7)).
Таким образом,
(см. формулу (8.7)).
Таким образом,
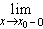 ax =
ax =
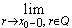 ar =
ar = 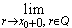 ar =
ar = 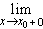 ax.
ax.
В силу равенства односторонних пределов
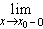 ax
=
ax
= 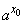 =
= 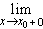 ax
ax
согласно теореме 2 из п.
6.6 существует двусторонний предел
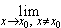 ax
=
ax
= 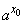 .
.
Отсюда в силу леммы 5
из п. 6.9 следует, что в точке x0 предел
функции ax существует и без
ограничения x x0,
т. е.
x0,
т. е.
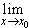 ax = ax = 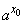 . .
|
(8.15) |
Это и означает, что функция ax, x  R,
непрерывна в любой точке x0
R,
непрерывна в любой точке x0  R.
R.
Доказательство 3o. Пусть сначала y = p -
натуральное число; тогда, применив p раз
свойство 2o, получим
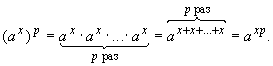
|
(8.16) |
Если y = 1/q, где q -
натуральное число, то
В самом деле, согласно определению корня для
доказательства справедливости равенства (8.17)
надо показать, что
(ax/q)q = ax,
а это равенство сразу следует из свойства (8.16):
(ax/q)q |
= |
a(x/q)q = ax. |
|
(8.16) |
|
Если y = p/q, где p и q -
натуральные числа, то
(ax)p/q = [(ax)p]1/q
|
= |
(axp)1/q |
= |
axp/q. |
(8.18) |
|
(8.16) |
|
(8.17) |
|
|
Если же y = -p/q, то
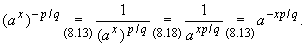
|
(8.19) |
Наконец, при y = 0, очевидно,
(ax)0 = 1 = a0
= 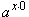 . . |
(8.20) |
Таким образом, для любого рационального числа r
справедливо равенство
Пусть теперь y - произвольное
действительное число. Возьмем какую-либо
последовательность рациональных чисел {rn},
имеющую своим пределом число y, т. е. rn y, rn
y, rn  Q, n = 1,
2, ... Тогда
Q, n = 1,
2, ... Тогда
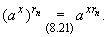
|
(8.22) |
Поскольку 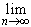 xrn =
xy, то в силу непрерывности функции ax
на всей числовой оси имеет место равенство
xrn =
xy, то в силу непрерывности функции ax
на всей числовой оси имеет место равенство
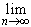 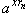 = axy. = axy.
|
(8.23) |
а в силу определения (8.7) степени числа -
равенство
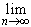 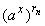 = (ax)y. = (ax)y.
|
(8.24) |
Переходя к пределу при n
 в равенстве (8.22), в силу (8.23) и
(8.24) получим (ax)y = axy.
в равенстве (8.22), в силу (8.23) и
(8.24) получим (ax)y = axy.
Доказательство. 5o. Поскольку
функция ax строго монотонная, то для
того чтобы доказать, что ее областью значений
является бесконечный интервал (0,+ ), надо согласно теореме
4 п. 7.3 доказать, например, при a > 1,
что
), надо согласно теореме
4 п. 7.3 доказать, например, при a > 1,
что
Эти пределы (конечные или
бесконечные) в силу монотонности функции всегда
существуют (см. п. 6.11),
поэтому достаточно лишь доказать, что для
каких-либо фиксированных последовательностей xn -
- и xn
и xn +
+ имеют место
равенства
имеют место
равенства 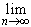
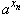 = 0,
= 0, 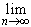
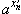 = +
= + , например, что эти равенства
справедливы для последовательностей xn = n
и x'n = n, n = 1, 2, ... А
это было доказано выше (см. пример 4
в п. 5.1).
, например, что эти равенства
справедливы для последовательностей xn = n
и x'n = n, n = 1, 2, ... А
это было доказано выше (см. пример 4
в п. 5.1).
Функция, обратная к
показательной функции y = ax,
a > 0, a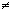 1,
называется логарифмической и обозначается loga y.
В силу свойства 5o показательной функции
логарифм loga y определен для любого
положительного числа. Число a называется основанием
логарифмической функции y = loga x.
Особую роль в математическом анализе играет
логарифмическая функция с основанием a = e,
она обозначается ln x и называется натуральным
логарифмом.
1,
называется логарифмической и обозначается loga y.
В силу свойства 5o показательной функции
логарифм loga y определен для любого
положительного числа. Число a называется основанием
логарифмической функции y = loga x.
Особую роль в математическом анализе играет
логарифмическая функция с основанием a = e,
она обозначается ln x и называется натуральным
логарифмом.
Согласно определению обратной функции
справедливо тождество
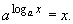
|
(8.26) |
Теорема. Логарифмическая функция y = loga x,
a > 0, a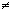 1,
определена и непрерывна при любом x > 0.
При этом она строго возрастает при a > 1
и строго убывает при 0 < a < 1.
1,
определена и непрерывна при любом x > 0.
При этом она строго возрастает при a > 1
и строго убывает при 0 < a < 1.
 Это непосредственно следует
из свойств 1o ,4o и 5o
показательной функции (теорема 3) и теоремы 4 из п. 7.3.
Это непосредственно следует
из свойств 1o ,4o и 5o
показательной функции (теорема 3) и теоремы 4 из п. 7.3. 
Подчеркнем, что нами, в частности,
доказано, что при любом основании a > 0,
a 1, логарифм loga x
определен для любого положительного числа x.
Из свойств 2o и 3o показательной
функции следуют соответствующие свойства
логарифма произведения и степени:
1, логарифм loga x
определен для любого положительного числа x.
Из свойств 2o и 3o показательной
функции следуют соответствующие свойства
логарифма произведения и степени:
Докажем, например, формулу (8.28). Согласно
свойству 3o показательной функции из
теоремы 3 имеем
Поэтому
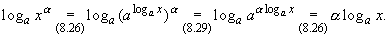
Из формул (8.27) и (8.28) следует формула для
логарифма частного:
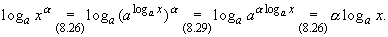
С помощью перечисленных свойств
показательной и логарифмической функций можно
получить и другие их свойства. Докажем, например,
равенство
(ab)x = axbx,
a > 0, b > 0
В случае a = 1, или b = 1
написанное равенство очевидно. Если же a 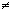 1 и b
1 и b 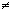 1, то
1, то
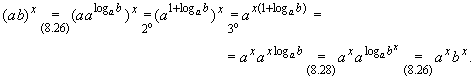
Многочлены и рациональные
функции Оглавление Степенная функция