Семинар 10. Радиоактивность

    Явление радиоактивности коренным образом изменило наше представление об устойчивости материи. Оказалось, что один химический элемент самопроизвольно без внешнего воздействия может превращаться в другие химические элементы. Превращение химических элементов является следствием радиоактивного распада атомных ядер.

10.1. Радиоактивный распад

10.2. α-распад

10.3. β-распад

10.4.  γ-распад

10.5. Энергии частиц в распадах

         Задачи

10.1. Радиоактивный распад

    Радиоактивный распад возможен тогда, когда он сопровождается выделением энергии. Масса М исходного ядра должна превосходить сумму масс  продуктов распада М > ∑_i m_i. Это условие является необходимым, но не всегда достаточным. Распад может быть запрещен другими законами сохранения − сохранения момента количества движения, электрического заряда, барионного заряда и т.д.
    Радиоактивный распад характеризуется временем жизни радиоактивного изотопа, типом испускаемых частиц, их энергиями, а при вылете из ядра нескольких частиц еще и относительными углами между направлениями вылета частиц.

Основные виды радиоактивного распада:

• α-распад – испускание ядрами α-частиц,
• β-распад – испускание (или поглощение) электрона и антинейтрино или позитрона и нейтрино,
• γ-распад – испускание γ-квантов,
• спонтанное деление – распад ядра на два осколка сравнимой массы.

    К более редким видам радиоактивного распада относятся испускание ядрами одного или двух протонов, а также испускание кластеров – лёгких ядер от углерода ¹²С до серы ³²S. Во всех видах радиоактивности, кроме γ‑распада, изменяется состав ядра – число протонов Z , массовое число А или и то и другое.

10.2. Альфа-распад

    Явление α-распада состоит в том, что тяжелые ядра самопроизвольно испускают α-частицы.

(A,Z) → (A-4, Z-2) + ⁴He.

    Характерные особенности α‑распада:
а)  α-распад происходит на тяжелых ядрах с Z > 60.
б) Периоды полураспада известных α-радиоактивных ядер варьируются в широких пределах. Так, изотоп вольфрама ¹⁸²W имеет период полураспада T_1/2 > 8.3·10¹⁸ лет, а изотоп протактиния ²¹⁹Pa – T_1/2 = 5.3·10^-8 c.
    Энергия a-распада

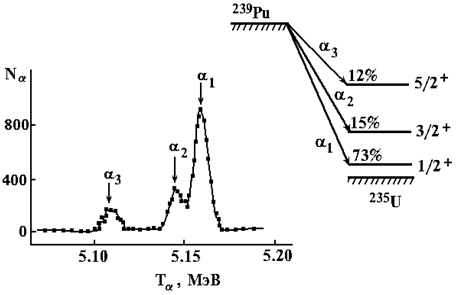
    Так как m_α << М, основная часть энергии α-распада уносится α-частицей и лишь ≈ 2% - конечным ядром. Тонкая структура α‑спектров связана с образованием конечного ядра не только в основном, но и в возбуждённых состояниях, т.е. α-спектры несут информацию об уровнях ядер.

Рис. 10.1. Энергетический спектр α-частиц, испускаемых плутонием ²³⁹Pu, и схема соответствующих α-переходов.

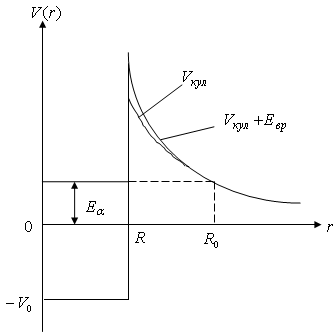
    Согласно теории Гамова, основным фактором, влияющим на время жизни a-активного ядра, является вероятность прохождения α-частицы через потенциальный барьер. Пусть внутри ядра радиуса R существует α-частица массы m_α. На рисунке 10.2 схематично изображен потенциал, в котором она находится. Постоянная распада l пропорциональна вероятности туннелирования α-частицы через потеαнциальный барьер:

(10.2)

где μ = m_αM_ядр/(m_α + M_ядр) ≈ m_α  − приведенная масса системы.

Рис. 10.2. Потенциальный барьер α-распада.

    Высота центробежного барьера , как правило, значительно ниже высоты кулоновского барьера, однако эта добавка может существенно влиять на вероятность распада.
    Установленная зависимость позволила объяснить эмпирический закон Гейгера-Неттола, связывающий период полураспада T_1/2 и кинетическую энергию α-частицы T_α:

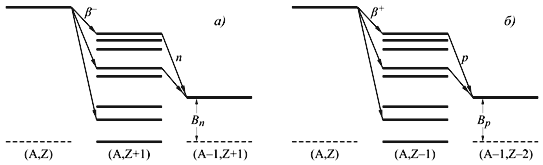
10.3. Бета-распад

    Существуют три типа β-распада − β^--распад, β⁺-распад и е-захват:

   β^-:  (A, Z) → (A, Z+1) + e^- + _e,
   β⁺: (A, Z) → (A, Z-1) + e⁺ + ν_e,
е: (A, Z) + e^- → (A, Z-1) + ν_e.

    Главной особенностью β-распада является то, что он обусловлен слабым взаимодействием. Бета-распад − процесс не внутриядерный, а внутринуклонный. В ядре распадается одиночный нуклон.

β^- (n → p + e^- + _e),              M(A, Z) > M(A, Z+1) + m_e,
β⁺ (p → n + e⁺ + ν_e),                M(A, Z) > M(A, Z-1) + m_e,
  e-захват (p + e^- → n + ν_e),       M(A, Z) + m_e > M(A, Z-1).

Энергия β-распада, выраженная через массы ядер,

Она заключена в интервале от 18.61 кэВ для распада трития (³H → ³He + e^- + _e) до 13.4 МэВ для распада тяжелого изотопа бора (¹²B → ¹²C + e^- + _e).
    При прочих равных условиях отношение вероятностей w_l и w₀ вылета пар лептонов с относительным орбитальным моментом l_eν = l и l_eν = 0:

wl/w0 ≈ (R/)2l.

(10.5)

    Типичные энергии β-распада Q_β ≈ 1 МэВ. При R ≈ 5 Фм

R/ = R·p/ћ ≈ R·Q_β/ћc ≈ 0.02.

Это объясняет наблюдающееся снижение вероятности β-распада на несколько порядков при возрастании на единицу l_eν.
    В результате β-распада ядра (A,Z+1) и (A,Z-1) могут образоваться в возбужденном состоянии. Если энергия возбужденных ядер (A,Z+1), (A,Z-1) больше энергии отделения протона или нейтрона, из этих состояний может происходить испускание протонов или нейтронов. Испускание протонов и нейтронов происходит практически мгновенно после того, как произошел предшествующий β-распад.

Рис. 10.3. Испускание запаздывающих частиц а) нейтронов, б) протонов

10.4. Гамма-распад

Рис. 10.4. Гамма-переходы между двумя уровнями ядра

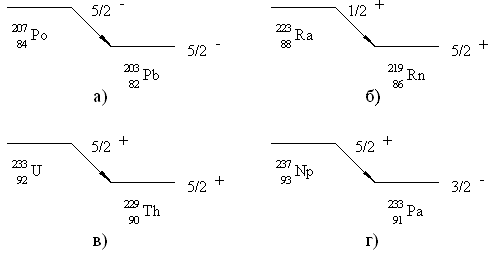
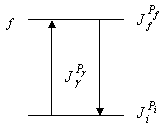
    Явление γ-распада ядер состоит в том, что ядро испускает γ‑квант без изменения массового числа А и заряда ядра Z. Гамма-излучение возникает при распаде возбужденного состояния ядра. Спектр γ-излучения всегда дискретен из-за дискретности ядерных уровней.

Гамма-переходы происходят между ядерными состояниями, характеризующимися определенными значениями спина J и чётности P. Поэтому испускаемые γ-кванты также имеют определённые значения J^P.

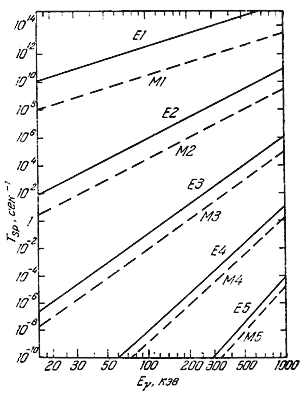
    В зависимости от чётности при определенном J фотоны различают по типу на магнитные (MJ) и электрические (EJ):

P = (-1)^J+1 − магнитные фотоны (МJ);
P = (-1)^J  − электрические фотоны (ЕJ).

    Вероятности вылета (или поглощения) магнитных и электрических фотонов подчиняются следующим приближенным соотношениям

(10.7)

Рис. 10.5.  Скорости γ-переходов (в сек^-1) протона в зависимости от энергии γ-квантов различных мультипольностей для ядра с A ≈ 100

    Времена жизни γ-радиоактивных ядер обычно не более 10^-7÷10^-11 с. В редких случаях при сочетании высокой степени запрета с малой энергией перехода могут наблюдаться γ-радиоактивные ядра с временами жизни до нескольких часов, а иногда и больше. Такие долгоживущие возбужденные состояния ядер называются изомерами.
    Изомерные состояния следует ожидать там, где оболочечные уровни, близкие друг другу по энергии, сильно различаются значениями спинов. Именно в этих областях и находятся так называемые «острова изомерии».
    Внутренняя конверсия. Ядро, находящееся в возбужденном состоянии, может перейти в основное состояние не только путем испускания γ-кванта, но и посредством передачи энергии возбуждения одному из электронов атомной оболочки. Такой процесс носит название внутренней конверсии и фотон, участвующий в нем, является виртуальным. Внутренняя конверсия − процесс, конкурирующий с γ‑излучением.
    Энергия внутренней конверсии электрона E_e равна энергии E ядерного возбуждения, уменьшенной на энергию ε связи электрона в атомной оболочке:

Рис. 10.6. Диаграмма механизма внутренней конверсии.

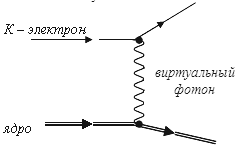
    Моноэнергетичность вылетающих при внутренней конверсии электронов позволяет отличить их от β-распадных электронов, спектр которых непрерывен.
    Внутренняя конверсия сопровождается рентгеновскими квантами, образующимися при переходе одного из наружных электронов на вакансию в K- или L-оболочке, освобожденную вылетевшим из атома электроном.

    Эффект Мессбауэра. При излучении γ-квантов ядро получает отдачу, что приводит к уменьшению энергии γ-кванта. В случае, если атомное ядро связано в кристаллической структуре, отдачу получает весь кристалл. Это явление получило название эффект Мессбауэра. С его помощью можно измерять энергию γ-квантов с относительной точностью ΔΕ/Е ~ 10^-17. Эффект Мессбауэра имеет многочисленные практические применения.

10.5. Энергии частиц в распадах

    Получим расчетные формулы для энергий частиц, образующихся в результате  α-, β- и γ- распадов.

    Альфа-распад представляет собой двухчастичный распад C(A,Z) → ⁴He + B(A-4, Z-2), где A и Z − массовое число и заряд ядра C. Известно, что энергия α-распада Q = (m_C − (m_α + m_B)c² составляет несколько МэВ, что много меньше масс продуктов распада. Тогда, используя соотношение
m_C ≈ m_α + m_B, из (1.38) получим для кинетической энергии α-частицы

(10.9)

и для энергии отдачи дочернего ядра

(10.10)

    Бета-распад представляет собой трехчастичный распад:

β^--распад:  C(A,Z) → B(A, Z+1) + e^- + _e
β⁺-распад: C(A,Z) → B(A, Z-1) + e⁺ + ν_e

    Максимальная отдачи дочернего ядра соответствует случаю, когда импульсы электрона (позитрона) и антинейтрино (нейтрино) сонаправлены

(10.11)

 и энергия антинейтрино (нейтрино) E_ν ≈ 0, тогда

(10.12)

Так как << Q, Q ≈ T_e + E_ν и максимальные энергия электрона (позитрона) и антинейтрино (нейтрино)

≈≈ Q.

    Таким образом, приближенно значение максимальной энергии нейтрино совпадает с верхней границей спектра β-распада и спектр нейтрино зеркально симметричен спектру электронов
N_ν(E) = N_e(Q − E).
    Третий случай β-распада, e-захват C(A,Z) + e^- → B(A, Z-1) + ν_e, поскольку T_e << m_e, фактически соответствует двухчастичному распаду системы с массой m_С + m_e. Спектр продуктов распада носит дискретный характер, согласно (1.37) энергия отдачи дочернего ядра

T_B = Q²/(2m_Cc²) 

и энергия нейтрино:

    Гамма-распад представляет собой процесс излучения γ-квантов ядром, находящимся в возбужденном состоянии. Энергия  γ-перехода

Q = m_i − m_f  = m_я + E_i − (m_я + E_f) = E_i − E_f,

где m_i, m_f, E_i, E_f − массы и энергии возбуждения начального и конечного состояний ядра
(m_i,f,с² >>E_i,f). Энергия ядра отдачи

T_я = Q²/(2m_яc²),

энергия γ-квант

E_γ ≈ Q.

Задачи

10.1. Получите расчетные формулы для энергий частиц, образующихся в результате  α-, β- и γ- распадов.

10.2. Активность препарата ³²P равна 2 мкКи. Сколько весит такой препарат?

10.3. Определите верхнюю границу возраста Земли, считая, что весь имеющийся на Земле ⁴⁰Ar образовался из ⁴⁰K в результате e-захвата. В настоящее время на каждые 300 атомов ⁴⁰Ar приходится один атом ⁴⁰K.

10.4. Определите сечение σ реакции ³¹P(n,p)³¹Si, если известно, что после облучения мишени ³¹P толщиной d = 1 г/см² в потоке нейтронов J = 2·10¹⁰ с^-1·см^-2 в течение времени t_обл = 4 ч ее
β-активность I, измеренная через время t_охл = 1 час после окончания облучения, оказалась
I(t_охл) = 3.9·10⁶ распадов/с. Период полураспада T_1/2(³¹Si) = 157.3 мин. 

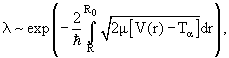
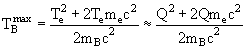
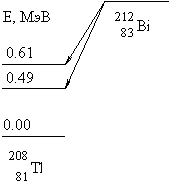10.5. Определите кинетические энергии α-частиц T_α, образующихся при α-распаде ²¹²Bi на возбужденные состояния ядра ²⁰⁸Tl с энергиями 0.49 и 0.61 МэВ. Энергия связи E_св(A,Z) ядра ²¹²Bi − 1654.32 МэВ, ядра ²⁰⁸Tl − 1632.23 МэВ и α-частицы − 28.30 МэВ.

10.6. Определите орбитальный момент l, уносимый α-частицей в следующих распадах:

10.7. Используя значения масс атомов, определите верхнюю границу спектра позитронов, испускаемых при β⁺ -распаде ядра ²⁷Si. M_ат(²⁷Si) = 25137.961 МэВ, M_ат(²⁷Al) = 25133.150 МэВ (массы в энергетических единицах).

10.8. Определите энергию отдачи ядра ⁷Li, образующегося при e-захвате в ядре ⁷Be. Даны энергии связи ядер - E_св(⁷Be) = 37.6 МэВ, E_св(⁷Li) = 39.3 МэВ.

10.9. Определите степень запрета β–распада скандия ⁴⁸Sc из основного состояния (J^P(Sc) = 6⁺).

10.10. Определите типы и мультипольности γ-переходов: 1)1^- → 0⁺; 2) 2⁺ → 3⁺.

10.11. Ядро кальция ⁴⁰Cа поглощает E1 γ-квант. Какие одночастичные переходы возможны?

10.12. Оцените доплеровское уширение спектральной линии с энергией E_γ = 1 МэВ при комнатной температуре (T = 300 K).  

10.13. Рассчитайте количество свинца, образовавшегося из 500 г изотопа урана ²³⁸U за время равное возрасту Земли (4.5 млрд. лет). Какой стабильный изотоп свинца образуется?
Ответ: ²⁰⁶Pb, m = 217 г

10.14. Период полураспада радиоактивного источника равен 1 минуте. В начальный момент его активность составляла 2·10³ Бк. Определите среднее время жизни и постоянную распада. Определите активность источника в моменты времени t = 1 мин, 2 мин, 3 мин, 10 мин. Определите число оставшихся радиоактивных ядер. 
Ответ:  λ = 0.693 мин^–1, τ = 1.44 мин, 1) A(1) = 10³ Бк, N(1) = 86.5·10³;
2) A(2) = 500 Бк, N(2) = 43.3·10³; 3) A(3) = 250 Бк, N(3) = 21.6·10³  4) A(10) = 1.95 Бк, N(10) = 162.8

10.15. Период полураспада радия ²²⁶Ra составляет 1620 лет. Вычислите число распадов 1 г изотопа за 1 год.
Ответ: N_расп = 1.14·10¹⁸ расп

10.16. Постоянная распада урана ²³⁵U равна  9.8·10^-10 год^-1. Вычислите период полураспада ²³⁵U. Сколько распадов происходит в течение 1 секунды в 10^-6 г ²³⁵U?
Ответ: T_1/2 = 7.1·10⁸ лет, N_расп = 0.08

10.17. Определить энергию W, выделяемую 1 мг препарата полония ²¹⁰Po за время, равное среднему времени жизни, если в одном акте распада выделяется энергия E = 5.4 МэВ.
Ответ: W = 1.6·10¹⁴ эрг

10.18. Радиоактивный источник неодима ¹⁴⁴Nd имеет массу 53.94 г и испускает 2.36 α‑частиц в секунду. Определите период полураспада и постоянную распада ¹⁴⁴Nd.
Ответ: T_1/2 = 2.2·10¹⁵ лет, λ =1.05·10^–23  с^–1

10.19. Образец руды содержит 0.85 г изотопа ²⁰⁶Pb на каждый грамм ²³⁸U. Определите возраст образца руды.
Ответ: t = 4.4·10⁹ лет

10.20. Рассчитайте энергию Т_α α-частицы и энергию отдачи Т_А-4 дочернего ядра при α‑распадах следующих ядер: 1) тория ²³²Th, 2) висмута  ²¹²Bi, 3)  урана ²³⁵U, 4) полония ²¹⁰Po, 5) америция ²⁴¹Am, 6) радона ²¹²Rn.
Ответ: T_α, T(A-4): 1) 3.92 МэВ, 69 кэВ; 2) 6.11 МэВ, 118 кэВ; 3) 4.60 МэВ, 80 кэВ;
4) 5.32 МэВ, 103 кэВ; 5) 5.54 МэВ, 94 кэВ; 3) 6.26 МэВ, 120 кэВ

10.21. Запишите реакцию и определите орбитальный момент, уносимый α‑частицей при α‑распадах следующих ядер: 1) урана ²³³U, 2) америция  ²⁴³Am, 3)  франция ²²¹Fr, 4) калифорния ²⁴⁹Cf.

10.22. Изотоп нептуния ²³³Np распадается с испусканием α‑частиц. Может ли ²³³Np распадаться с испусканием протонов или нейтронов? Объясните полученный результат.

10.23. Почему нет стабильных атомных ядер с A = 5 и A = 8?

10.24. 1) Радиоактивное семейство 4n + 3 начинается с распада урана ²³⁵U и заканчивается образованием свинца ²⁰⁷Pb. Сколько α‑ и β‑распадов происходит в этой цепочке распадов? Вычислите полную энергию, выделяющуюся при распаде всей цепочки изотопов. Перечислите все образующиеся изотопы.
2) В условиях задачи 1) рассмотрите радиоактивный ряд радия 4n + 2 (от урана ²³⁸U до свинца ²⁰⁶Pb);
3) В условиях задачи 1) рассмотрите радиоактивный ряд радия 4n + 1 (от нептуния ²³⁷Np до висмута ²⁰⁹Bi);
4) В условиях задачи 1) рассмотрите радиоактивный ряд радия 4n (от урана ²³⁶U до свинца ²⁰⁸Pb);
Ответ: 1) 7α + 4β, W = 46.4 МэВ; 2) 8α + 6β, W = 51.7 МэВ; 3) 8α + 4β, W = 49.3 МэВ;
4) 6α + 4β, W = 42.7 МэВ

10.25. Изотоп радона ²²²Rn испускает α-частицы, имеющие скорость 1.6·10⁷ м/с. Вычислите импульс и кинетическую энергию α-частицы.
Ответ:  p = 198.95 МэВ/c, T_α = 5.31 МэВ

10.26. Изотоп радия ²²⁶Rа испускает α‑частицы с энергиями 4.78 МэВ и 4.60 МэВ. Нарисуйте схему распада этого изотопа и рассчитайте энергии γ‑квантов, которые испускаются при α‑распаде.
Ответ: E_γ ≈ 0.19 МэВ

10.27. Ядра радона ²¹⁹Rn из основного состояния испускает α‑частицы с энергиями 6.817 МэВ,
6.551 МэВ, 6.423 МэВ и 6.211 МэВ и γ‑кванты с энергиями 0.128 МэВ, 0.210 МэВ, 0.267 МэВ, 0.340 МэВ и 0.605 МэВ. Какое ядро образуется в результате α‑распада? Постройте схему уровней дочернего ядра.
Ответ:  ²¹⁵Po, E^*: 271 кэВ, 402 кэВ, 608 кэВ

10.28. Какой тип распада можно ожидать у следующих ядер: 1) гелия ⁶He; 2) бериллия ⁸Be; 3) углерода ¹⁵C;  4) бериллия ¹³Be; 5) хлора ³⁶Cl? Напишите схему реакции и рассчитайте энергию распада.  

10.29. Какие моды распада возможны для следующих изотопов: 1) меди ⁶⁴Cu;    2) ванадия ⁵⁰V;
3) марганца ⁵⁴Mn; 4) родия ¹⁰⁴Rh; 5) иода ¹²⁸I; 6) цезия ¹³²Cs? Напишите схему реакции и рассчитайте энергию распада.

10.30.  Используя значения масс атомных ядер, определите верхнюю границу спектра β⁺-распада, максимальную энергию вылетевшего нейтрино и максимальную отдачу дочернего ядра при распаде ядер: 1) калия ⁴⁰K; 2) меди ⁶⁴Cu; 3) мышьяка ⁷⁴As; 4) рубидия ⁸²Rb; 5) индия ¹¹¹In; 6) иода ¹²⁴I.

10.31. Следующие ядра могут распадаться в результате е-захвата: 1) бериллий ⁷Be, 2) бор ⁸B;              3) углерод ¹⁰C; 4) фтор ¹⁷F; 5) натрий ²¹Na; 6) скандий ⁴²Sc. Какие ядра образуется в этих распадах? Вычислите импульс нейтрино и энергию образовавшегося дочернего ядра. 

10.28-31.  Проверить результаты можно по базам ядерных данных

10.32. Найти верхнюю границу спектра позитронов в β⁺-распадах 1) ¹⁵O, 2) ¹¹C, 3) ¹³N,  4) ¹⁸F.  и определить значения суммарного полного момента пары испущенных лептонов.  
Ответ: 1) Q = 1.73 МэВ, J_eν = 0,1; 2) Q = 0.96 МэВ, J_eν = 0÷3; 3) Q = 1.20 МэВ, J_eν = 0,1; 
4) Q = 0.63 МэВ, J_eν = 1

 10.33.  Определите порядок запрета следующих β-распадов: 1) ²⁶Al(5⁺) → ²⁶Mg*(2⁺);
2)²⁶Si(0⁺) → ²⁶Al*(0⁺) → ²⁶Mg(0⁺); 3) ⁸⁷Rb(3/2^-) → ⁸⁷Sr(9/2⁺) ; 4) ⁴⁰K(4^-) → ⁴⁰Ca(0⁺).
Ответ: 1) 2; 2) разрешенные переходы типа Ферми; 3) 3; 4) 3.

10.34. Определить типы и мультипольности γ‑переходов: 1) 2^- → 0⁺, 2)  2⁺ → 2⁺, 3) 1⁺ → 0⁺,
4) 1/2⁺  → 5/2^-,  5) 2⁺ → 3^-, 6) 3/2⁺ → 5/2⁺.

10.35. Возможны ли  γ-переходы между состояниями с нулевыми полными моментами количества движения?

10.36. За счет каких процессов в ядре могут осуществляться следующие переходы: 1) 0^- → 0⁺; 2) 0⁺ → ⁰⁺; 3) 0^- → 0^-; 4) 0⁺ → 0^- ?

10.37. Определить энергию Е_γ, мультипольность и четность γ-кванта и кинетическую энергию отдачи ядра  при излучении γ-кванта возбужденным ядром ¹²C^*, находящимся в первом возбужденном состоянии J^P = 2⁺ с энергией E^* = 4.43 МэВ.
Ответ: E2, E_γ = 4.43 МэВ; T_C = 0.88 кэВ

10.38. Какие одночастичные переходы возможны при поглощении фотонов следующими ядрами:       1) углерода ¹²C – Е1 γ-кванта; 2) кислорода ¹⁶O – Е2 γ-кванта;  3) углерода ¹⁴C – M1 γ-кванта;    4) кремния  ²⁸Si – Е1 γ-кванта?

10.39. Какую энергию отдачи получает ядро ⁵⁷Fe при испускании γ-кванта с энергией 14.4 кэВ?
Ответ: T(Fe) = 2·10^–3  эВ

10.40. Рассчитайте ширину спектральной линии при γ-распаде бора ¹¹B из возбужденного состояния с энергией 2.12 МэВ, если время жизни этого состояния 3·10^-15 с.
Ответ: Γ = 0.22 эВ

10.41. Серебряная пластина толщиной d = 0.1 мм и площадью S = 20 см² облучалась в течение 5 минут в потоке тепловых нейтронов интенсивностью 5·10⁷ нейтронов/см². Определите активность A пластины в конце облучения. Плотность серебра 10,5 г/см², соотношение изотопов: ¹⁰⁷Ag – 51.35%, ¹⁰⁹Ag – 48.65%, сечения активации: σ(¹⁰⁷Ag) = 45 б, σ(¹⁰⁹Ag) = 45 б.
Ответ: A = 1.15 мКи

10.42. В ядерный реактор, производящий поток тепловых нейтронов с интенсивностью 10¹⁵ нейтронов/см²·с, на 30 часов помещен образец кобальта ⁵⁹Co. Исследования на масс-спектрометре показали, что образец содержит 0,22% ⁶⁰Co. Определить сечение активации ⁵⁹Co.
Ответ: σ = 20.4  б

10.43. Какова будет активность A изотопа ¹⁵O, образующегося в мишени ¹²C толщиной d = 0.1 мг/см² после ее облучения в течение 4 минут α-частицами с энергией 14,6 МэВ. Ток пучка 20 нА. Сечение реакции ¹²С(α,n)¹⁵O при данной энергии σ = 25 мб. Т_1/2(¹⁵O) ≈ 2 мин.
Ответ:  A = 6·10³ Бк