Атом водорода
Hydrogen Atom
Атом водорода
– связанная система, состоящая из положительно заряженного ядра – протона
и отрицательного заряженного электрона.
Размеры атома определяются размерами его электронной оболочки
≈ 10-8 см.
Энергии связанных состояний электрона получаются при решении
уравнения Шредингера с потенциалом
![]()
где n – главное квантовое число, определяющее энергии различных состояний
электрона в атоме водорода (n = 1, 2, 3…), R - постоянная Ридберга
(R = 1.0974·105 см-1).
Каждому уровню с главным квантовым числом n соответствует n состояний,
различающихся квантовыми числами l = 0, 1, 2, …, (n-1). Такое вырождение
уровней по энергии характерно только для кулоновского поля. Кроме того,
каждое из этих вырожденных по l состояний (2l+1)-кратно вырождено по магнитному
числу
m = ±l, ±(l-1),...±1, 0. Таким образом, полная кратность вырождения
стационарного квантового состояния с главным квантовым числом n дается соотношением
![]() .
.
Такое рассмотрение справедливо при условии, что спин электрона
равен нулю. Так как электрон имеет спин s = 1/2, полный момент количества
движения
![]() электрона
будет определяться векторной суммой его орбитального
электрона
будет определяться векторной суммой его орбитального
![]() и спинового
и спинового
![]() моментов
моментов
![]() =
=
![]() +
+
![]() .
.
Так как спин электрона s = 1/2, его полный момент количества
движения J может быть только полуцелым.
При заданном значении орбитального
момента l в атоме водорода возможно два состояния, различающихся значениями
полного момента
![]() =
=
![]() +
+
![]() = l
+ 1/2 и
= l
+ 1/2 и
j = l - s = l - 1/2. Эти два значения различаются взаимными ориентациями
орбитального и спинового векторов. Энергии электрона в состояниях l + 1/2
и l - 1/2 в кулоновском поле протона несколько отличаются, и вырождение
по энергии состояний снимается. Это дополнительное взаимодействие носит
название спин-орбитального. С учетом снятия вырождения спектр низколежащих
состояний атома водорода обогащается, происходит тонкое расщепление уровней
энергий. Вместо двух низших уровней водорода без учета спин-орбитального
расщепления (основного 1s и первого возбужденного 2s2p (рис. 1, а)) с учетом
спин-орбитального расщепления их становится четыре (рис. 1, б). Квантовые
характеристики этих уровней даны в таблице. Уровень с большим значением
j = l + 1/2 расположен выше по энергии, чем уровень с j = l - 1/2. Состояния
с различными значениями l, но одним и тем же значением nj оказываются по-прежнему
вырожденными. Например, 2s1/2 и 2p1/2.
 Рис. 1. Схема уровней атома водорода: а – без учёта спина электрона и спина ядра, б – тонкое расщепление уровней, учитывающее спин электрона, в - сверхтонкое расщепление уровней, учитывающее взаимодействие магнитного момента электрона с магнитным моментом ядра. Лэмбовский сдвиг уровней 2s1/2 и 2р1/2 ~4·10-6 эВ. Положения уровней и величины их расщеплений даны не в масштабе |
Квантовые характеристики электрона в самых нижних
состояниях атома водорода
| n | l | s | j = l ± s | обозначение уровней |
| 1 | 0 | 1/2 | 1/2 | 1s1/2 |
| 2 | 0 1 |
1/2 1/2 |
1/2 1/2, 3/2 |
2s1/2 2p1/2, 2p3/2 |
| 3 | 0 1 2 |
1/2 1/2 1/2 |
1/2 1/2, 3/2 3/2, 5/2 |
3s1/2 3p1/2, 3p3/2 3d1/2, 3d3/2 |
Из точного решения релятивистского уравнения Дирака для электрона со спином s = 1/2 следует зависимость энергии уровней атома водорода от квантовых чисел n и j
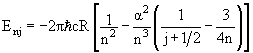 ,
,
где α = 1/137 - постоянная тонкой структуры. Поправка в Enj не зависит от квантового числа l. Поэтому энергии состояний с одинаковыми j и разными l должны быть равны. Величина тонкого расщепления уровней δEj+1,j при данном n определяется соотношением
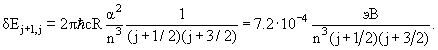
Величина расщепления уровня с n = 2 составляет ≈ 4.5·10-5
эВ.
Ядро атома водорода – протон - также имеет собственный момент
– спин s = 1/2. Это тоже слегка изменяет взаимодействие электрона с протоном,
так как возникает дополнительное взаимодействие магнитного момента протона,
вызванного наличием у него спина, с магнитным полем электрона. Величина
этого взаимодействия зависит от взаимной ориентации спинового момента протона
и полного момента электрона. Таким образом, возникает еще один тип расщепления
уровней атома, называемого сверхтонким, так как его величина существенно
меньше тонкого расщепления. Сверхтонкое расщепление будет наблюдаться уже
для основного состояния
(n = 1, l = 0). Переход между двумя подуровнями
сверхтонкого расщепления основного состояния водорода приводит к излучению
с длиной волны λ = 21 см (частота излучения 1420 МГц). С помощью этого излучения
обычно регистрируется межзвездный водород во Вселенной.
Состояния от n = 2 до n = ∞ называются возбужденными состояниями.
Энергия возбуждения Eвозб (энергия, которую необходимо сообщить
системе, чтобы она перешла из начального состояния ni в конечное
состояние nf) определяется из соотношения
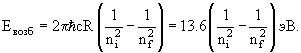
Все состояния от n = 1 до n = ∞ являются связанными состояниями, так
как имеют отрицательные энергии. При приближении n к бесконечности энергии
состояний сближаются, и разница в энергиях соседних состояний становится
настолько мала, что расщепленные уровни сливаются, и дискретный спектр уровней
трансформируется в непрерывный (сплошной). Когда энергия электрона становится
положительной (E > 0), система превращается в несвязанную и электрон становится
свободным. Спектр энергий свободного электрона непрерывный.
Переходы из состояний n = 2, 3, … ∞ в состояние n = 1 образуют
серию Лаймана. Переходы из состояния n = 3, 4, … ∞ в состояние n = 2 – серию
Бальмера. Переходы между состояниями с отрицательной энергией (E < 0) приводят
к образованию дискретного спектра переходов, в то время как переходы между
состояниями с E > 0 и состояниями с E < 0 дают непрерывный спектр переходов.
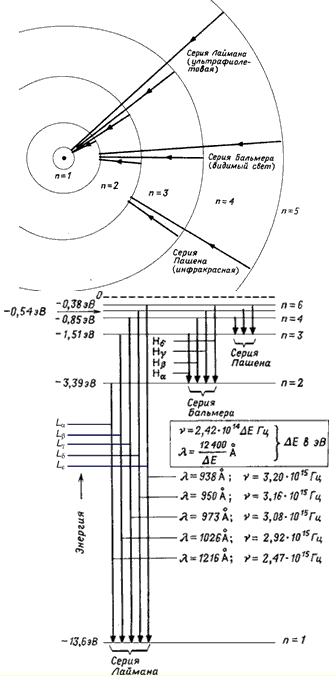
Рис. 2. Схема уровней атома водорода.
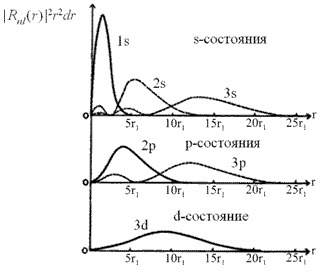 Рис. 3. Радиальное распределение вероятности |Rnl(r)|2r2dr нахождения электрона в кулоновском поле протона (атом водорода) в s, p и d состояниях. Расстояния даны в боровских радиусах r1 = ћ2/mee2 ≈ 0.529·10-8 cм. |
Согласно точному решению уравнения Дирака, уровни
энергии с одинаковым значением квантового числа n = 1, 2, 3,... и одинаковым
значением полного момента
j = 1/2, 3/2,... должны совпадать по энергии независимо
от значения квантового числа l. В 1947 г.
У.
Лэмб и Р. Ризерфорд обнаружили сдвиг уровней 2s1/2
и 2p1/2 в атоме водорода. Этот сдвиг уровней называется
лэмбовским сдвигом. Основная причина
лэмбовского сдвига обусловлена радиационными поправками:
- Испусканием связанным электроном виртуальных фотонов.
- Поляризацией вакуума — рождением в вакууме электрон-позитронных пар.
Эти две поправки полностью объясняют наблюдаемую величину
лэмбовского сдвига уровней 2s1/2 и 2p1/2 (ΔE
= 4.5·10-6 эВ).
Вероятность dw нахождения электрона в объеме dV в определенном
месте пространства определяется выражением
dw = |ψ(x, y, z)|2 dV = |Rnl(r)Ylm(θ,φ)|2r2sinθdθdφdr
=
= |Rnl(r)|2r2 |Ylm(θ,φ)|2sinθdθdφdr,
распадается на радиальную вероятность ||Rnl(r)|2r2|2r2dr и угловую - |Ylm(θ,φ)|2dΩ. Распределения этих вероятностей даны на рис. 3–5.
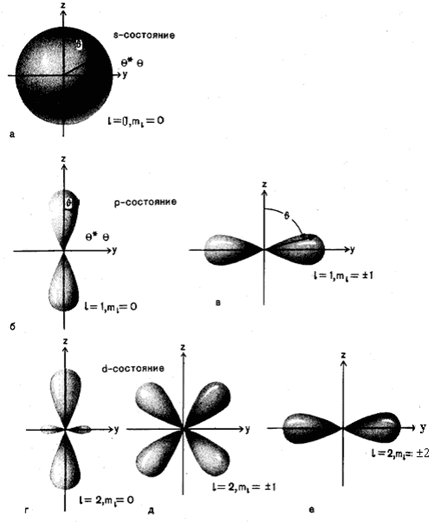 Рис. 4. Распределение угловой вероятности |Ylm(θ,φ)|2dΩ нахождения частицы в s, p и d состояниях в сферически симметричном потенциале |
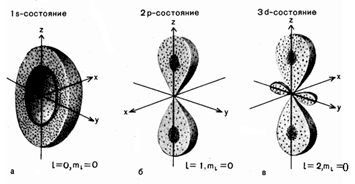 Рис. 5. Распределение полной вероятности |