Сферическая система координат
Spherical Coordinate System

    Сферическая система координат широко используется при решении задач со сферически симметричным потенциалом

V = V(r).

Связь между переменными (x,y,z) прямоугольной и (r,θ,φ) сферической систем координат

x = rsinθcosφ,
y = rsinθsinφ,
z = rcosθ

показана на рис. Элементу объёма в прямоугольной системе координат dxdydz соответствует элемент объёма r²sinθdθdφdr в сферической системе координат.

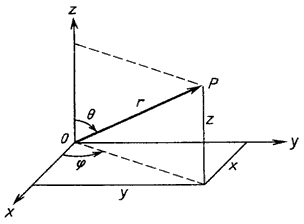Рис. Прямоугольная и сферическая системы координат.

    В сферических координатах стационарное уравнение Шредингера для частицы в центральном потенциале U(r) имеет вид

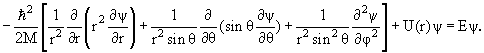(1)

Волновая функция ψ(r,θ,φ), являющаяся решением уравнения (1), имеет вид произведения радиальной и угловой функций

где радиальная функция R_nl(r) и угловая функция Y_lm(θ,φ) удовлетворяют уравнениям

2Ylm(θ,φ) = ћ2l(l + 1)Ylm(θ,φ),

(3а)

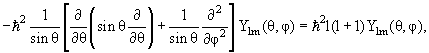(3б)

и

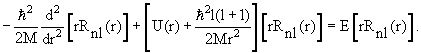(4)

    Уравнение (3а) определяет возможные собственные значения и собственные функции Y_lm(θ,φ) оператора квадрата момента ². Уравнение (4) определяет собственные значения энергии Е и радиальные собственные функции R_nl(r).
    Решения уравнения (1) существуют лишь при определенных значениях квантовых чисел n (радиальное квантовое число), l (орбитальное квантовое число) и m (магнитное квантовое число). Возможные энергетические состояния системы (уровни энергии) определяются числами n и l. Число n может быть только целым, сколь угодно большим: n = 1, 2, …, ∞. Число l может принимать значения l = 0, 1, 2, …, ∞.

Собственные значения L² и L_z являются решением операторных уравнений

²Y_lm(θ,φ) = L²Y_lm(θ,φ) и _zY_lm(θ,φ) = L_zY_lm(θ,φ).

Они имеют следующие дискретные значения

L² = ћ²l(l + 1), где l = 0, 1, 2, 3, …,
L_z = ћm, где m = 0, ±1, ±2, ±3,…, ±l.

Сферические функции (их называют также сферическими гармониками) Y_lm(θ,φ) являются собственными функциями операторов ² и _z, т. е. описывают состояния с определенными l и m, а значит и определенными значениями орбитального момента и его проекции на ось z. Сферические функции Y_lm(θ,φ) описываются формулой

 ,

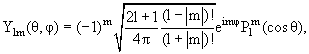где - функция Лежандра.

Свойства сферических функций Y_lm(θ,φ):

Симметрия:

Y_lm(π−θ,φ+π) = (-1)^lY_lm(θ,φ),
Y^*_lm(θ,φ) = (-1)^mY_l,-m(θ,φ).

Ортогональность:

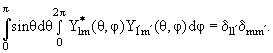
В качестве примера ниже приведены сферические функции Y_lm(θ,φ) для l = 0, 1, 2: