Орбитальный момент
Angular Momentum
Орбитальный момент
- момент количества движения частицы, обусловленный её движением в пространстве.
Величина орбитального момента количества движения L дается соотношением
L2 = ћ2l(l + 1),
l - орбитальное квантовое число.
Обычно, для упрощения, когда говорят о величине орбитального
момента количества движения, называют этой величиной число l, имея в виду,
что между l и L имеется однозначная связь L2 = ћ2l(l
+ 1).
Так как величина l может принимать только целочисленные значения
0, 1, 2, 3,…, то и орбитальный момент количества движения квантуется. Например,
для частицы с l = 2 момент количества движения
![]()
Для сравнения укажем, что орбитальный момент количества движения Земли
вокруг Солнца больше в ~1074 раз.
Для характеристики состояний с различными значениями орбитального
числа l обычно используют спектроскопические названия орбитальных моментов
в соответствии со следующей таблицей.
Таблица. Спектроскопические названия орбитальных чисел l
| l = 0 | s-состояние |
| l = 1 | p-состояние |
| l = 2 | d-состояние |
| l = 3 | f-состояние |
| l = 4 | g-состояние |
| l = 5 | h-состояние |
| и т. д. | |
Состоянию с l = 0 отвечает сферически симметричная волновая функция. В тех случаях, когда l ≠ 0 волновая функция не имеет сферической симметрии. Симметрия волновой функции определяется симметрией сферических функций.
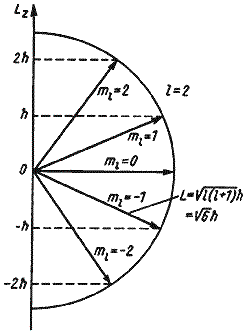
Рис. Возможные ориентации вектора
![]() при
орбитальном квантовом числе l = 2.
при
орбитальном квантовом числе l = 2.
Орбитальный момент количества движения является векторной
величиной. Так как величина орбитального момента количества движения квантуется,
то и направление
![]() по
отношению к выделенному направлению z, например, к внешнему магнитному полю,
также квантуется (это называют пространственным квантованием). Проекция
на это направление принимает дискретные значения Lz = ћm, где
m изменяется от +l до –l, т. е. имеет 2l+1 значение. Например, при
l = 2
величина m принимает значения +2, +1, 0, -1, -2 (рис.). Энергия сферически
симметричной системы не зависит от m,
по
отношению к выделенному направлению z, например, к внешнему магнитному полю,
также квантуется (это называют пространственным квантованием). Проекция
на это направление принимает дискретные значения Lz = ћm, где
m изменяется от +l до –l, т. е. имеет 2l+1 значение. Например, при
l = 2
величина m принимает значения +2, +1, 0, -1, -2 (рис.). Энергия сферически
симметричной системы не зависит от m,
т. е. от направления вектора
![]() .
.
См. также