Волновое уравнение
_{Wave equation}

    Волновое уравнение − линейное дифференциальное уравнение в частных производных, описывающее малые колебания струны, колебательные процессы в сплошных средах и в электродинамике.
    В общем случае волна, распространяющаяся в пространстве, описывается уравнением

(1)

где u = u(x,y,z,t) − возмущение в точке x,y,z в момент времени t, v − скорость распространения волны. Уравнение (1) инвариантно относительно замены v → -v.
    Монохроматическая волна − распространение колебаний с определённой частотой ω. В случае одномерного распространения волны вдоль оси x формула монохроматической волны имеет вид

u(x,t) = Asin(ωt − xv).

Длина волны λ − путь, пройденный возмущением (состоянием с определённой фазой) за время равное периоду колебаний T

λ = vT.

Волновое число

k = 2π/λ.

Частота ω и период колебаний T связаны соотношением

ω = 2π/T.

    Эквивалентные формулы для монохроматической волны, распространяющейся вдоль оси x

u(x,t) = Asin(ωt − kx) = Asinω(t − x/v) = Asin2π(t/T − x/λ).

    Сферическая волна.

u(r,t) = (A/r)sin(ωt − kr).

    Стоячая волна. При наложении монохроматических волн одинаковой частоты образуется устойчивая картина результирующих колебаний с характерными максимумами и минимумами.

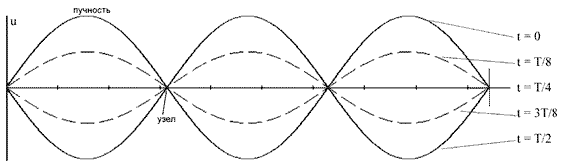
    Стоячая волна образуется в системах с двумя жёстко закреплёнными точками. При отражении фаза волны меняется на π и происходит интерференция падающей и отраженной волн.

    Соотношение (2) можно получить, используя формулу

sinα − sinβ = 2sin[(α − β)/2] cos[(α + β)/2] 

и положив 2Asin(2πx/λ) = A(x), A(x) − амплитуда стоячей волны.