Осциллятор
_Oscillator

    Осциллятор – система, тело, частица, совершающие периодические колебания вокруг положения устойчивого равновесия. В классической физике частота колебаний гармонического осциллятора , где m – масса осциллятора, а k – некая постоянная (например, жёсткость пружины), определяющая масштаб возвращающей (к положению равновесия) силы F = - kx (x – отклонение от положения равновесия). Энергия классического осциллятора пропорциональна квадрату амплитуды его колебаний и может изменяться непрерывно.
    Квантовый осциллятор описывается гамильтонианом

    Уровни энергии гармонического осциллятора E_n и волновые функции ψ_n(x,t) определяются из уравнения Шредингера

E_n = ћω(n+1/2),  n = 0, 1, 2, …

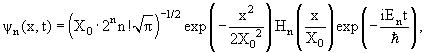
– амплитуда нулевых колебаний,
H_n(x) – полиномы Эрмита

    Квантовые осцилляции, реализующиеся в молекулах, атомах, ядрах, могут происходить лишь при фиксированном наборе отдельных энергий, т.е. спектр уровней такого осциллятора дискретен. Уровни квантового осциллятора эквидистантны и даются выражением Е_n = ћω(n + 1/2), где n = 0, 1, 2, …, а ћ = h/2π (h – постоянная Планка). n иногда называют числом фононов. Наинизшая энергия квантовых осцилляций (энергия его нулевых колебаний) Е₀ = ћω/2 > 0. Таким образом, квантовый осциллятор нельзя остановить (для этого его надо уничтожить). Значение ω, определяющее основной тон квантового осциллятора, связано с его потенциальной энергией классическим соотношением mω²x²/2 = kx²/2.
    Под влиянием внешнего возмущения квантовый осциллятор может переходить с одного уровня на другой. При этом минимальная энергия поглощаемых и излучаемых квантов (энергия одного фонона) равна ћω.

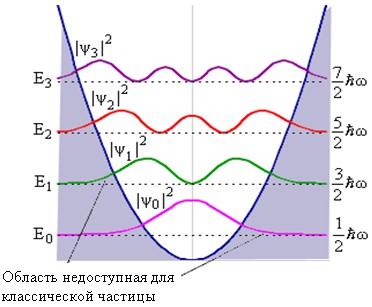
Рис. Спектр энергий и квадраты модулей волновых функций квантового гармонического осциллятора.