Чарм. Чармоний
Charm. Charmonium
Чарм c - аддитивное
квантовое число, характеризующее кварки и адроны. Частицы с ненулевым значением
квантового числа с называются очарованными частицами. В их состав входит
с- или 
-кварк.
Квантовое число чарм с сохраняется в сильных и электромагнитных взаимодействиях
Δc = 0. В слабых распадах очарованных частиц квантовое число с не изменяется
или изменяется на единицу Δc = 0,±1. Самыми лёгкими очарованными частицами
является семейство D мезонов, состоящее из комбинации лёгких u,
,
d,
кварков,
с и кварков.
| D0 = (c) |
D+ = (c) |
|
D0
= (u) |
D− = (d) |
Чармоний - семейство тяжёлых мезонов
со скрытым очарованием, т.к. оно состоит из с- и
-кварков
и потому имеет квантовое число с = 0. Первым мезоном из семейства частиц
со скрытым очарованием был J/ψ-мезон, открытый в 1974 г. J/ψ-мезон имеет
массу M = 3.097 ГэВ, спин J = 1, отрицательную внутреннюю чётность P = -1.
Позднее было открыто большее число частиц, состоящих из с-кварков.
Классификация чармониев основана на кварковой модели адронов. При одинаковом
кварковом составе (с)
они различаются главным квантовым числом n, суммарным спином J кварка с
и антикварка
, чётностью
P и зарядовой чётностью C. P- и C-чётности различных состояний чармония
определяются соотношениями
P = (-1)L+1, C = (-1)L+S.
|
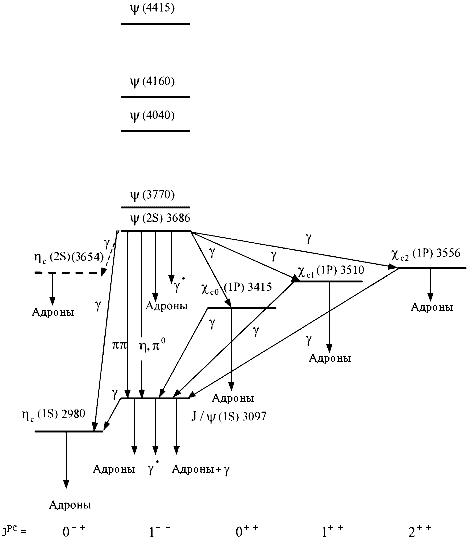
Рис. 1 Система уровней чармония и переходы между состояниями |
На рисунке показана система уровней чармония и переходы
между ними. Характерный масштаб возбуждения составляет сотни МэВ, что существенно
меньше массы с-кварка. Поэтому можно воспользоваться тем, что движение нерелятивистское
и для описания чармония использовать уравнение Шредингера. В таком подходе
чармоний можно рассматривать как систему двух кварков, движущихся в потенциале
V(r). Состояния чармония и волновые функции определяются как решения станционарного
уравнения Шредингера.
Для описания спектроскопии чармония удалось найти простой потенциал
V(r). На малых расстояниях (r << 10-13 см) потенциал, аналогично
кулоновскому, имеет вид V(r) ~ 1/r. Поскольку кварки не наблюдаются в свободном
состоянии, потенциал должен их эффективно «запирать» на расстояниях масштаба
радиуса адрона (≈10-15 м), т.е. на больших расстояниях потенциал
должен расти (V(r) ~ r). Удовлетворяющий требуемым условиям потенциал имеет
вид
,
где a, β, δ - константы. Константы удалось подобрать так, что потенциал
одновременно хорошо описывает спектры масс как (c),
так и (b
).
См. также